Linear Regression Analysis in ML

Linear Regression in AI

• Linear regression is a statistical regression method which is used for predictive analysis.
• It is one of the very simple and easy algorithms which works on regression and shows the relationship between the continuous variables.
• It is used for solving the regression problem in machine learning.
• Linear regression shows the linear relationship between the independent variable (X-axis) and the dependent variable (Y-axis), hence called linear regression.
• If there is only one input variable (x), then such linear regression is called simple linear regression. And if there is more than one input variable, then such linear regression is called multiple linear regression.

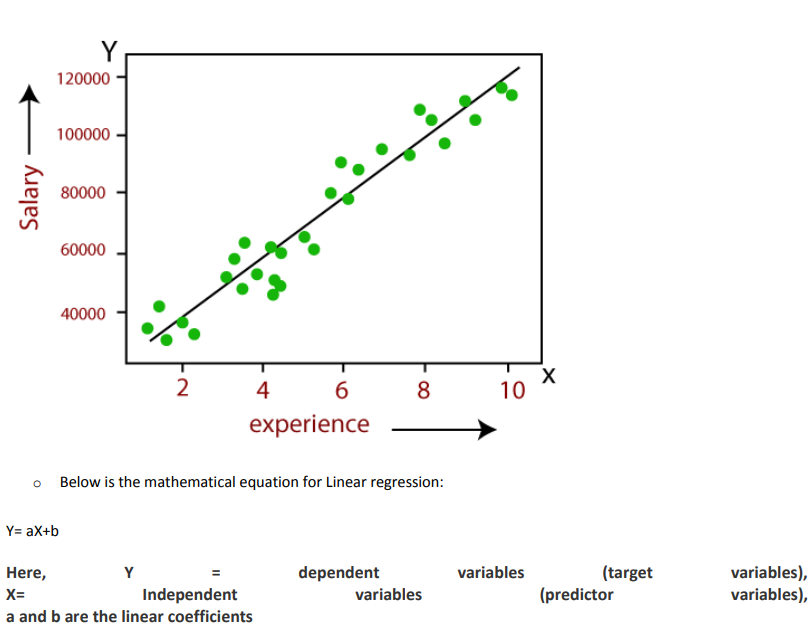
The relationship between variables in the linear regression model can be explained using the below image. Here we are predicting the salary of an employee on the basis of the year of experience

Some popular applications of linear regression are:
o Analyzing trends and sales estimates
o Salary forecasting
o Real estate prediction
o Arriving at ETAs in traffic

Types of Linear Regression

#1. Simple Linear Regression

If a single independent variable is used to predict the value of a numerical dependent variable, then such a Linear Regression algorithm is called Simple Linear Regression.

#2. Multiple Linear regression

If more than one independent variable is used to predict the value of a numerical dependent variable, then such a Linear Regression algorithm is called Multiple Linear Regression.

Linear Regression Line

A linear line showing the relationship between the dependent and independent variables is called a regression line. A regression line can show two types of relationship:

#1. Positive Linear Relationship

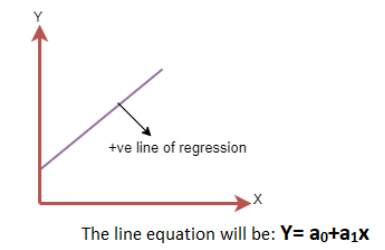
If the dependent variable increases on the Y-axis and independent variable increases on X-axis, then such a relationship is termed as a Positive linear relationship.

#2. Negative Linear Relationship

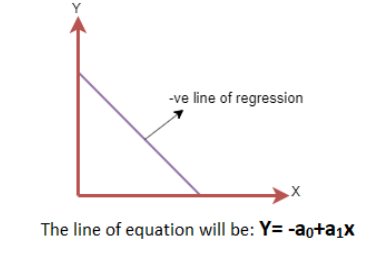
If the dependent variable decreases on the Y-axis and independent variable increases on the X-axis, then such a relationship is called a negative linear relationship.

Finding the best fit line:

When working with linear regression, our main goal is to find the best fit line that means the error between predicted values and actual values should be minimized. The best fit line will have the least error.

The different values for weights or the coefficient of lines (a0, a1) gives a different line of regression, so we need to calculate the best values for a0 and a1 to find the best fit line, so to calculate this we use cost function.

Cost function:

• The different values for weights or coefficient of lines (a0, a1) gives the different line of regression, and the cost function is used to estimate the values of the coefficient for the best fit line.
• Cost function optimizes the regression coefficients or weights. It measures how a linear regression model is performing.
• We can use the cost function to find the accuracy of the mapping function, which maps the input variable to the output variable. This mapping function is also known as Hypothesis function.

For Linear Regression, we use the Mean Squared Error (MSE) cost function, which is the average of squared error occurred between the predicted values and actual values. It can be written as:

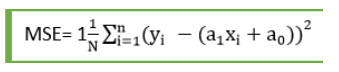
Where, N=Total number of observation, Yi = Actual value, (a1xi+a0)= Predicted value